| menu |
 |
| Home :: |
 |
| Matlab :: |
 |
| Fan regulator :: |
 |
| Sumo robotów :: |
 |
| :: |
 |
| :: |
 |
| Kontakt :: |
 |
 |
ZASTOSOWANIA MATLABA
Poniżej zamieszczam opis kilku zagadnień, jakie przyszło mi rozwiązywać z użyciem Matlaba. W większości są tą problemy z zakresu automatyki i robotyki, chociaż część z nich da się z pewnością zastosować w innych dziedzinach.
Piszcie, co interesuje Was w tym narzędziu - mam dużo pomysłów na rozbudowywanie tej strony, ale nie starczyłoby mi na nic więcej czasu :).
SPIS TREŚCI
1. Podstwy matlaba.
2. Funkcje i skrypty.
3. Przekształcenia jednorodne.
4. Składanie przekształceń.
5. Nakładanie łatek.
6. Obliczanie kątów Eulera.
7. Identyfikacja obiektów sterowania.
8.Dostęp do portów i innych urządzeń z poziomu Matlaba (w przygotowaniu).
Czym jest matlab?
Najkrócej rzecz ujmując, matlab jest interpretatorem. Pozwala na uruchamianie skryptów napisanych w specyficznym dla tego środowiska języku. Można także wydawać mu pojedyncze polecenia – działa wtedy jak linia poleceń dosu. Zoptymalizowany jest do obliczeń inżynierskich, ale można go bez problemu stosować w najprzeróżniejszych dziedzinach. Co ważne, podstawowym sposobem reprezentacji danych są tu macierze (matlab = mat(rix)+lab(oratory))
W kilku następnych artykułach spróbuję przybliżyć Wam podstawy obsługi matlaba, programowanie w nim, oraz jego praktyczne zastosowanie w różnych dziedzinach.
Ponieważ matlab został przewidziany do skomplikowanych obliczeń, nie mamy tu najmniejszych problemów z rozwiązywaniem wielu problemów matematycznych. Udostępniono nam funkcje całkowania, różniczkowania, badanie transmitancji widmowych, rozwiązywanie równań i wiele, wiele innych. Na potrzeby kilku pierwszych artykułów zajmiemy się rachunkiem macierzowym, który okaże się niezbędny podczas tworzenia animacji.
Mamy do wykorzystania pełne spektrum operacji macierzowych dostępnych bezpośrednio jako funkcje matlaba.
Przykład:
» a=[1 2 4
5 2 4
1 0 1]
a =
1 2 4
5 2 4
1 0 1
» a^-1
ans =
-0.2500 0.2500 0
0.1250 0.3750 -2.0000
0.2500 -0.2500 1.0000
Zademonstrowałem operację odwracania macierzy a. Opisy wszystkich podstawowychoperacji są dostępne po wpisaniu np. help * w linii poleceń matlaba. Bardziej rozbudowane funkcje wykonywane na macierzach również są dostępne. Przykładem jest sortrows(x,c) która pozwala na posortowanie wzrastająco macierzy x względem kolumny c. Te i kilka innych funkcji wykorzystamy podczas tworzenia ruchomej grafiki.
Podstawą do tworzenia programów w matlabie są funkcje i skrypty. Jedne i drugie mają postać plików tekstowych ASCII i działają prawie tak samo, jak wpisanie serii poleceń do głównego okna matlaba. Na nasz użytek oddany został edytor z funkcjami zbliżonymi do tych umieszczonych w kompilatorach np. C++.
Między funkcjami i skryptami występują między innymi następujące różnice:
- uruchomienie skryptu daje identyczny wynik, jak ręczne wpisanie komend w nim zawartych do
linii poleceń – funkcje się tak nie zachowują,
- dane utworzone w skrypcie są dostępne w środowisku matlaba (jeśli w naszym workspace istnieje zmienna a, a skrypt wydaje polecenie
utworzenia również zmiennej a, to zmienna z workspace zostanie nadpisana i vice
versa),
- dane funkcji są jej wewnętrznymi danymi, nie ma do nich dostępu z zewnątrz (od tej reguły występują wyjątki, ale o tym później),
- nie możemy kompilować skryptów (o kompilacji w następnym
artykule).
Oto przykład prostej funkcji zrealizowanej w środowisku matlaba:
function
[s]=srednia(x)global s;
suma=0;
for i=1:lenght(x),
suma=suma+x(i);
end;
s=suma/lenght(x);
Ta prosta funkcja pozwala wyliczyć średnią z liczb zawartych w wektorze x (jak wspomniałem, matlab z natury dobrze
radzi sobie z danymi wektorowymi i macierzowymi). Funkcja oparta jest na pętli,
korzysta dodatkowo z innej funkcji length(x) zwracającej ilość elementów
wektora x. Poza tym mamy tu dane wejściowe, jak i dane wyjściowe (co nie ma
miejsca zawsze) co pozwala nam zaobserwować, jak wygląda składnia definiowania
funkcji – pozostałe elementy nie różnią się od komend wpisywanych do okna
matlaba.
By skorzystać z danej funkcji piszemy na przykład:
y=srednia([2
4 1 5])
w odpowiedzi dostaniemy wartość y = 3. W tym przypadku naszym wektorem wejściowym x jest [2 4 1 5]. Zauważmy, że
w matlabie elementy macierzy i wektorów rozdzielane są spacjami.
Powyższy przykład miał tylko na
celu pokazanie struktury funkcji, operacja obliczania średniej (jak i wiele
innych operacji statystycznych) dostępne są jako gotowe funkcje. Co ważniejsze,
struktura funkcji nie jest optymalna dla matlaba ponieważ matlab najszybciej
wykonuje operacje macierzowe, a nie pętle (w tej roli lepiej sprawdzają się
języki kompilowalne).
Komentarza wymaga również zapis global s. Jest to deklaracja zmiennej s jako globalnej. Ponieważ funkcje
ukrywają przed światem zewnętrznym swoje zmienne, nie mamy do nich bezpośredniego dostępu. W powyższym przykładzie uzyskaliśmy ten dostęp przez
przypisanie zmiennej y wartości funkcji srednia dla argumentu x (x = [2 4 1
5]).
Jeśli jednak funkcja nie generuje
danych wyjściowych w takiej postaci, możemy mieć do nich dostęp właśnie dzięki
deklaracji global. Powoduje ona, że zmienna s jest dostępna zarówno w
workspace, jak i dla innych funkcji. Jak się okaże wkrótce, dostępność pewnych
zmiennych jest czasami bardzo pożądana, zwłaszcza, gdy mamy do czynienia z
większymi programami wykorzystującymi interfejs graficzny i dużą ilość funkcji
(interfejs graficzny sam w sobie jest również funkcją, zazwyczaj wywoływaną bez
parametrów – o interfejsie będziecie mogli szerzej poczytać w dalszej części
artykułu).
Na koniec jeszcze dodam, że z naszej funkcji srednia skorzystamy dopiero wtedy, gdy podane wyżej instrukcje
umieścimy w pliku o nazwie srednia.m i umieścimy go na ścieżce dostępu matlaba.
Teraz kilka słów o skryptach. Jak wspomniałem wcześniej, skrypty są wykonywane identycznie, jak w przypadku ręcznego wpisywania komend do okna edycyjnego. Zmienne utworzone lub modyfikowane w skrypcie są ogólno dostępne. Nie ma możliwości korzystania ze skryptów w przypadku programów przeznaczonych do kompilacji. Jeśli zależy nam na użyciu jakiegoś skryptu w takim właśnie programie, wystarczy formalnie w nagłówku skryptu dodać nazwę funkcji i określić ją jako bezargumentową (np. srednia()). Tak samo jak w przypadku funkcji zmienne z workspace są dostępne.
3. Przekształcenia jednorodne.
Przekształcenia przestrzeni trójwymiarowej.
Tego rodzaju przekształcenia stosowane są w robotyce do obliczania
zadań prostych i odwrotnych manipulatorów robotów.
Zadanie proste polega na obliczeniu na podstawie zmiennych
kinematycznych (czyli obrotów i wysuwów odpowiednich członów robota)
położenia końcówki manipulatora (lub innego jego punktu) w globalnym
(zewnętrznym) układzie współrzędnych.
Zadanie odwrotne jest trudniejsze i obejmuje wyliczenie ustawień kątów
i wysuwów na podstawie zadanego położenia końcówki.
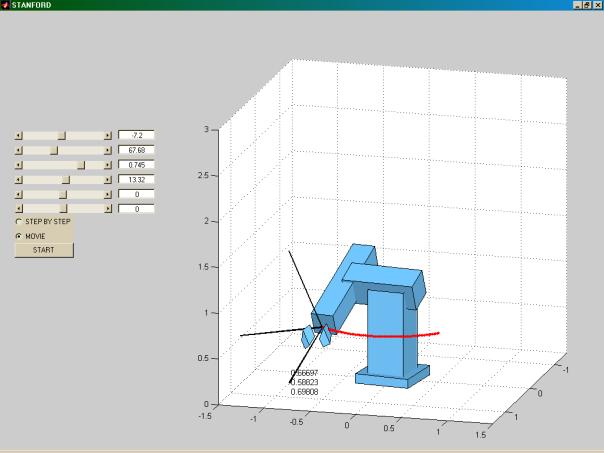
W pierwszej części akapitu zostały umieszczone informacje, jak za pomocą w/w przekształceń operować trójwymiarowymi obiektami. Druga część będzie opisem programu wyliczającego zadanie proste (i być może w niedalekiej przyszłości zadanie odwrotne) dla manipulatora typu stanfordzkiego.
By dokonać przekształceń obiektów w przestrzeni 3D będziemy stosować
homeogeniczne (jednorodne) przekształcenia macierzowe.
Na użytek tych przekształceń powstały współrzędne jednorodne. By przedstawić w tych współrzędnych klasyczne
współrzędne przestrzeni trójwymiarowej, stosujemy następujący zapis:
[x, y, z] (klasycznie) = [x/k,y/k, z/k, k] (wsp. jednorodne).
Łatwo zauważyć, że mnożenie takiego wektora przez skalar nie wpływa no położenie reprezentowanego przez
niego punktu. Poza tym, najczęściej wektory współrzędnych jednorodnych
przyjmują postać [x, y, z, 1]. Od tej pory współrzędne będziemy zapisywać w
takiej właśnie postaci.
Następne zagadnienie, jakie będziemy musieli rozważyć to liczba stopni swobody ciała w przestrzeni. Punkt w
sensie matematycznym posiada tylko 3 stopnie swobody (wsp. jego położenia).
Odcinek posiada pięć, a bryła – 6. Oprócz 3 współrzędnych położenia, bryła
posiada 3 współrzędne orientacji. Orientacja może być definiowana na różne
sposoby. Nas interesować będzie następująca reprezentacja macierzowa:
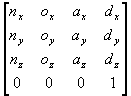
Ortonormalne (wzajemnie prostopadłe i o długości jednostkowej) wektory n, o, a tworzą lokalny układ
współrzędnych przywiązany do jakiegoś punktu naszego ciała. nx
stanowi długość (więc jest to skalar) rzutu wektora n na oś x
(zewnętrzny układ współrzędnych x, y, z jest również
ortonormalny), analogicznie dla innych osi.
Warto zwrócić uwagę, że jeżeli dwa
wektory mają długość równą jeden, to rzut jednego na drugi ma długość liczbowo
równą kosinusowi kierunkowemu kąta zawartego pomiędzy tymi wektorami. Dodatkowo
współrzędne dx, dy, dz dają informacje na
temat położenia początku lokalnego układu współrzędnych względem układu
głównego. Macierz pokazana powyżej definiuje nam w pełnia położenie i
orientację bryły w przestrzeni trójwymiarowej. Warto zaznaczyć, że informacja
ta jest nadmiarowa – mając pewne kosinusy kierunkowe, można wyznaczyć
pozostałe.
Myślę, że po tym wstępie możemy już zająć się konkretami.
Wiemy już, jak reprezentować
położenie bryły, teraz zajmiemy się pojedynczymi punktami oraz ich
przemieszczeniami. Podam teraz macierze, które pozwalają na obracanie punktu
(bryły, całego układu brył), względem osi x, y, z zewnętrznego układu
współrzędnych.
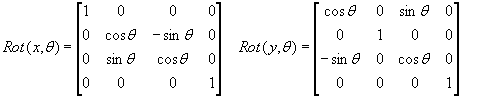
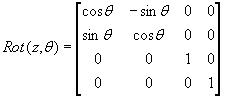
Z kolei macierz przesunięcia (bez dokonywania obrotu) będzie wyglądać następująco:
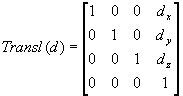
Inne złożenia mają bardziej skomplikowaną postać.
Teraz chyba najbardziej
wartościowe przekształcenie: obrót względem danej osi l o kąt q. Oś w tym
przypadku jest reprezentowana przez wektor (jednostkowy) l.
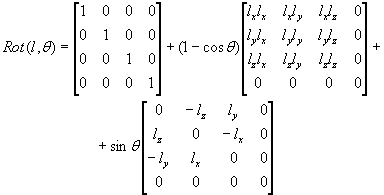
Nadmienię tylko, że oś obrotu l przechodzi przez początek zewnętrznego układu współrzędnych. Najwyższy czas wyjaśnić, w jaki sposób odbywają się wymieniane przeze mnie przekształcenia. Mając dane położenia interesujących nas punktów w przestrzeni reprezentowanych w postaci jednorodnej możemy za pomocą przekształceń jednorodnych dokonać ich transformacji (przesunięcia i/lub obrotu). Działanie to polega na mnożeniu jednorodnej reprezentacji wektora przez macierz przekształcenia. Rozważmy przykład: Obrócić punkt o współrzędnych [1, 1, 1] wokół osi Z o kąt 90. Łatwo wyobrazić sobie, że nowy punkt będzie miał współrzędne [-1, 1, 1] ale dokonajmy tego mnożenia:
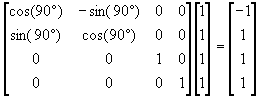
Jak widzimy otrzymane współrzędne są takie same, jak te przewidziane przez nas.
Myślę, że czas już zaprzątnąć do pracy komputer. Poniżej podaję listing funkcji matlaba pozwalającej na
obliczenie operatora przekształcenia (obrót + przesunięcie) względem dowolnie
wybranej osi:
function
[p]=operator(c1,c2,teta,tranx,trany,tranz);syms c3 p real;
c3=(1-c1^2-c2^2)^0.5;
subs(c3);
teta=teta*pi/180;
tran=[0 0 0 tranx
0 0 0 trany
0 0 0 tranz
0 0 0 1];
p1=[1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 0];
p1=p1*cos(teta);
p2=[c1*c1 c1*c2 c1*c3 0
c2*c1 c2*c2 c2*c3 0
c3*c1 c3*c2 c3*c3 0
0 0 0 0];
p2=p2*(1-cos(teta));
p3=[0 -c3 c2 0
c3 0 -c1 0
-c2 c1 0 0
0 0 0 0];
p3=p3*sin(teta);
p=p1+p2+p3+tran;
p=real(p);
Zainteresowanych tym, skąd biorą się poszczególne składniki (p1 – p3) przekształcenia odsyłam do miejsca gdzie podany był wzór na Rot(l,q) . Na tym etapie ważne jest tylko to, że wcześniej wymienione przekształcenie jest złożeniem (w tym przypadku jest to mnożenie macierzy) kilku odrębnych przekształceń.
Omówię teraz sposób korzystania z
powyższej funkcji:
- argumentami wejściowymi są c1, c2, teta, tranx, trany, tranz kolejno: kosinus
kierunkowy w kierunku osi X wersora osi obrotu, kosinus kierunkowy w kierunku
osi Y tegoż samego wersora, kąt obrotu, oraz 3 współrzędne przesunięcia
- wielkością wyjściową jest macierz przekształcenia
- kąt obrotu podajemy w stopniach
Szerszego omówienia wymaga zdefiniowanie osi obrotu. Na pytanie dlaczego do zdefiniowania osi obrotu użyto tylko dwóch współrzędnych odpowiadam: współrzędne te to współrzędne wersora tej osi. Pociąga to za sobą równość:
![]()
która zresztą jest uwidoczniona w 3. linii listingu. Zauważmy, że obliczona w ten sposób trzecia współrzędna ma
zawsze wartość nieujemną (jest to liczba rzeczywista). Co więc zrobić, jeśli
zależy nam na obrocie wokół osi, która skierowana jest w stronę ujemnych wartości Z? Radzimy sobie z tym w następujący sposób: zamiast obracać wokół osi
l = [x, y, -z] o kąt q, obracamy wokół osi [-x, -y, z] (przeciwnie skierowanej) o kąt -q.
Później wykażemy, że taka reprezentacja może być kłopotliwa, jeśli nasza funkcja jest
wykorzystywana przez inna funkcję, a my nie wiemy jakie są parametry wejściowe. Na razie
jednak ta forma jest bardziej dogodna.
Sprawdzimy teraz jak działa nasza funkcja. Zdefiniujemy zbiór punktów i dokonamy na nim przekształcenia. Całość
zobrazujemy na wykresie. Niech naszym zbiorem punktów będzie odcinek:
» for i=1:100,
punkty(1:3,i)=skala(i);
punkty(4,i)=1;
end
» rys=[punkty nowe];
» hold on
» plot3(nowe(1,1:100),nowe(2,1:100),nowe(3,1:100));
» plot3(punkty(1,1:100),punkty(2,1:100),punkty(3,1:100));
» axis([-5 5 -5 5 -5 5]);
» grid on
Teraz proszę skorzystać z obrotu
3D (przycisk na pasku narzędzi okna z wykresem) żeby sprawdzić, że faktycznie
jeden odcinek jest prostopadły względem drugiego w płaszczyźnie Z. W razie wątpliwości dotyczących funkcji użytych powyżej polecam wpisanie help ‘nazwa
funkcji’ w oknie matlaba.
Tym przykładem kończę wstęp do przekształceń jednorodnych. W następnej części składanie przekształceń, obrót
względem osi nie przechodzących przez początek układu i inne ciekawe tematy oraz przykład animacji.
Wspomniałem już wcześniej, że macierz przekształcenia umożliwia zarówno obrót jak i przesunięcie obiektu. Można
jednak działania te rozdzielić. Przykłady obrotów pokazałem wyżej. Macierz
samego przesunięcia również została przedstawiona. Teraz zobaczymy, co dzieje
się kiedy mnożymy przez siebie macierze przekształcenia. Weźmy pod uwagę dwa
przekształcenia obrót względem osi Z o 90°
oraz kolejny obrót względem tej samej osi, tym razem o -
180°.
Zobaczmy jaki jest wynik:
» operator(0,0,90,0,0,0)
ans =
0.0000
-1.0000 0
0
1.0000 0.0000 0
0
0
0 1.0000
0
0
0 0
1.0000
» operator(0,0,-180,0,0,0)
ans =
-1.0000
0.0000
0 0
-0.0000 -1.0000
0 0
0
0 1.0000 0
0
0
0 1.0000
»
Zobaczmy teraz jaki będzie wynik złożenia
tych przkształceń:
» operator(0,0,-180,0,0,0)*operator(0,0,90,0,0,0)
ans =
0.0000
1.0000 0
0
-1.0000
0.0000
0 0
0
0 1.0000 0
0
0
0 1.0000
»
A teraz sprawdźmy czy przypadkiem nie przewidzieliśmy tego rozwiązania:
» operator(0,0,-90,0,0,0)
ans =
0.0000
1.0000
0 0
-1.0000
0.0000
0 0
0
0 1.0000 0
0
0
0 1.0000
»
Otrzymaliśmy taki sam wynik.
Składanie przekształceń odpowiada więc kolejnemu wykonywaniu poszczególnych
przekształceń wchodzących w skład tego złożenia.Zauważmy, że składanie
przekształceń, to mnożenie macierzy przekształceń w kierunku od późniejszych
do wcześniejszych działań.Oznacza to, że operacja która ma być wykonana
ostatnia jest na pierwszym miejscu w złożeniu. Zaznaczę przy okazji, że
mnożenie macierzy jest łączne, ale nie jest przemienne. Później dowiemy
się, że składania przekształceń jest szczególnie przydatne tam, gdzie potrzebna
jest nam znajomość położenia jednego lokalnego układu współrzędnych względem
innego układu.
a=[5 0 0 1]';
skala=linspace(0,1000);
for i=1:100,
b(1:4,i)=operator(0,0,skala(i),0,0,skala(i)/180)*a;
end
plot3(b(1,1:100),b(2,1:100),b(3,1:100))
grid on
Uruchomiony bez parametrów
Archimedes daje nam taki wynik:
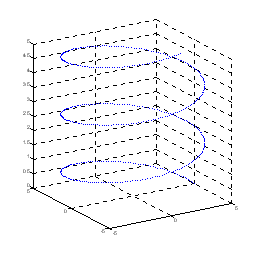
Teraz coś, co na pewno bardziej ucieszy oczy: ten sam problem przedstawiony w postaci animacji:
function Archimedes();
a=[5 0 0 1]';
skala=linspace(0,1000,500);
axis([-5 5 -5 5 0 5]);
grid on
hold on
for i=1:500,
b(1:4,i)=operator(0,0,skala(i),0,0,skala(i)/180)*a;
plot3(b(1,i),b(2,i),b(3,i))
drawnow;
end
W następnym przykładzie użyjemy sprzętowego przyspieszania animacji (OpenGL lub Zbuffer). Na razie jednak chciałbym was zapoznać z funkcją Patch i jej zastosowaniem w tworzeniu grafiki w matlabie.
Funkcja patch służy do
nakładania łatek na wielokąty (zarówno dwu- jak i trójwymiarowe). Jednak pomimo
trójwymiarowości wielokąty te muszą
leżeć w jakiejś płaszczyźnie. Podstawowa składnia patch
wygląda następująco: patch(współrzędne_x, współrzędne_y,
współrzędne_z,kolor). Współrzędne podawane są w postaci wektorów (dla
pojedynczej łatki) lub macierzy (w przypadku tworu „wielołatkowego” np.
sześcianu). Kolor podany jest w postaci wektora [r g b] przy czym poszczególne
litery oznaczają składowe czerwieni, zieleni oraz niebieskiego i są z
przedziału 0 – 1. Przykładowo kolor biały to [1 1 1], czarny [0 0 0], czysty
zielony [0 1 0]. Kolory można podawać także w postaci ‘kolor’. Możemy więc
zamiast [1 0 0] wpisać ‘r’ (red –
czerwony).
Teraz prosty przykład – rysowanie kwadratu:
patch([1 1 –1 –1],[1 –1 –1 1],’r’);
axis([-2 2 –2 2]);
axis equal;
Do grafiki trójwymiarowej wygodnie będzie napisać funkcję która poda nam w dogodnej formie współrzędne na przykład prostopadłościanu. Mówiąc w dogodnej formie miałem na myśli formę, która pozwoli na bezproblemowe nakładanie łatek na ten prostopadłościan. Funkcja taka będzie bardzo przydatna w tworzeniu obiektów o nieco większym stopniu skomplikowania. Oto przykład:
Na początek parametry funkcji:
rozmiary a, b, c. Pozycja środka symetrii: x, y, z. Zakładamy że a jest rozmiarem
w kierunku osi X, pozostałe wymiary analogicznie. Funkcja może wyglądać tak:
function [vertices,faces,punkty]=bryla(x,y,z,a,b,c);
figura=[x+a/2 y+b/2 z+c/2 1
x+a/2 y+b/2 z-c/2 1
x+a/2 y-b/2 z-c/2 1
x+a/2 y-b/2 z+c/2 1
x-a/2 y+b/2 z+c/2 1
x-a/2 y+b/2 z-c/2 1
x-a/2 y-b/2 z-c/2 1
x-a/2 y-b/2 z+c/2 1
x+a/2 y-b/2 z+c/2 1
x-a/2 y-b/2 z+c/2 1
x-a/2 y+b/2 z+c/2 1
x+a/2 y+b/2 z+c/2 1
x+a/2 y-b/2 z-c/2 1
x-a/2 y-b/2 z-c/2 1
x-a/2 y+b/2 z-c/2 1
x+a/2 y+b/2 z-c/2 1
x+a/2 y-b/2 z-c/2 1
x-a/2 y-b/2 z-c/2 1
x-a/2 y-b/2 z+c/2 1
x+a/2 y-b/2 z+c/2 1
x+a/2 y+b/2 z-c/2 1
x-a/2 y+b/2 z-c/2 1
x-a/2 y+b/2 z+c/2 1
x+a/2 y+b/2 z+c/2 1];
punkty=figura';
vertices=figura(1:24,1:3);
faces=[1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
17 18 19 20
21 22 23 24];
Dodatkowego komentarza wymaga trzeci parametr
wyjściowy: punkty. Jest to jednorodna reprezentacja punktów naszej bryły.
Dzięki tej reprezentacji będziemy mogli wykorzystać przekształcenia jednorodne
do wykonywania obrotów i przesunięć brył.
Oto przykład wykorzystania:
»
[a b c]=bryla(0,0,0,3,1,1);
» patch('vertices',a,'faces',b,'facevertexcdata',[0.4 0.7 0.9],'facecolor','flat');
»
axis ([-5 5 -5 5 -5 5])
Większość
z podanych wcześniej informacji posłuży teraz do napisania kilku użytecznych
programów.
Programy te w większości były projektami zaliczeniowymi na kierunku
Automatyka i Robotyka. Pierwszy z nich miał na celu wizualizację
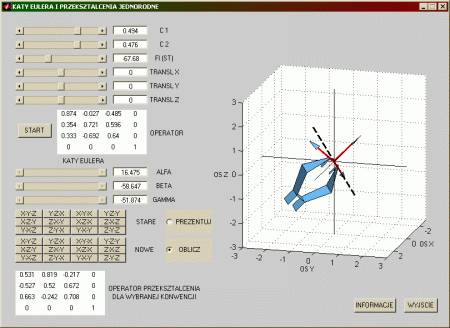
problemu obliczania kątów Eulera. Kąty te są sposobem określenia
orientacji bryły w przestrzeni trójwymiarowej. Jest aż 24 konwencji kątów
Eulera. Są to wszystkie możliwe kombinacje obrotów wokół osi. 12 z nich
dotyczy obracania wokół osi globalnych (zewnętrznych) układu współrzędnych.
Druga połowa konwencji dotyczy obracania wokół kolejnych osi lokalnego
(związanego z bryłą) układu współrzędnych.
W praktyce (na przykład w programowaniu robotów) najczęściej używa się
konwecji ZXZ lub ZYZ dla obrotów względem nowych osi. Oznacza to, że aby
bryła uzyskała zadaną orientację zostaną wykonane kolejno 3 obroty:
- obrót wokół osi Z o kąt alfa
- obrót wokół osi X (Y) o kąt beta
- obrót wokół osi Z o kąt gamma.
Wszystkie te obroty dokonują się wokół osi lokalnych (a więc
przemieszczających się razem z bryłą).
Ustalenie wzorów na kąty Eulera jest dość uciążliwe i zajęło
autorowi dobrych kilka godzin (mimo usilnych prób nie udało się znaleźć
gotowych rozwiązań w literaturze czy internecie).
Jak podałem wcześniej, aby doprowadzić ciało do zadanego położenia
należy podać kąty Eulera. Jest też inny, prostszy sposób: jedna oś,
wokół której obracamy ciało, aby zajęło odpowiednią pozycję. Tak więc
aby obliczyć kąty Eulera dla podanej orientacji, wybieramy dwa kosinusy
kierunkowe osi obrotu, oraz kąt obrotu (ze znakiem) i na tej podstawie
generujemy operator obrotu (patrz operator
obrotu wokół osi). Otrzymana macierz jest parametrem wejściowym
funkcji do obliczania kątów.
Funkcje obliczające kąty Eulera można pobrać tutaj.
Nie są to gotowe programy, ponieważ były używane
jako funkcje składowe w innym programie. Można jednak z nich wyłuskać
odpowiednie wzory (zajmują one kilka początkowych linijek każdego pliku).
Zainteresowanych napisaniem takiego lub podobnego programu lub/i
skorzystaniem z fragmentów przedstawianego programu proszę o kontakt (z
racji chęci zachowania praw autorskich nie zamieszczam na stronie całego
programu).
Program umożliwia obliczanie kątów Eulera a także prezentacje ruchu manipulatora wykonującego odpowiednie obroty. Mamy tutaj możliwość obliczenia kątów dla zadanej docelowej orientacji (dla wszystkich 24 konwencji), wykonanie obrotów dla 3 zdefiniowanych kątów i podanie operatorów obrotu dla każdego ruchu, a także dla sekwencji 3 ruchów.
7. Identyfikacja obiektów sterowania.
Tym razem zajmiemy się zagadnieniem znanym automatykom – identyfikacją obiektów sterowania. Najogólniej rzecz biorąc, celem identyfikacji jest rozpoznanie rzeczywistych parametrów obiektu, układu, zjawiska. Weźmy przykład: masa zawieszona na sprężynie. Nie znamy ani wartości masy, ani współczynnika sprężystości sprężyny. Pobudzamy taki układ i obserwujemy, jak się zachowuje. Na podstawie obserwacji szacujemy interesujące nas wielkości. Dokładnie rzecz biorąc powyższa metodologia sprowadza się zastosowania poniższego układu:
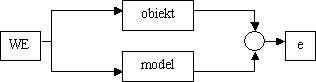
Od wyjścia obiektu jest odejmowane wyjście modelu a różnica ta stanowi uchyb.
W istocie schemat ten winien zawierać dodatkowo zakłócenie działające na obiekt oraz sprzężenie od e (epsilon) wpływające na
parametry modelu. Wszystkie metody identyfikacji polegają na tym, że uchyb e jest minimalizowany poprzez zmianę parametrów modelu. Jeśli
uchyb jest minimalny, oznacza to, że model jest prawie dokładnym odzwierciedleniem obiektu (o ideale nie może być mowy ze względu na zakłócenia
oddziaływujące na obiekt a przez to również na jego wyjście).
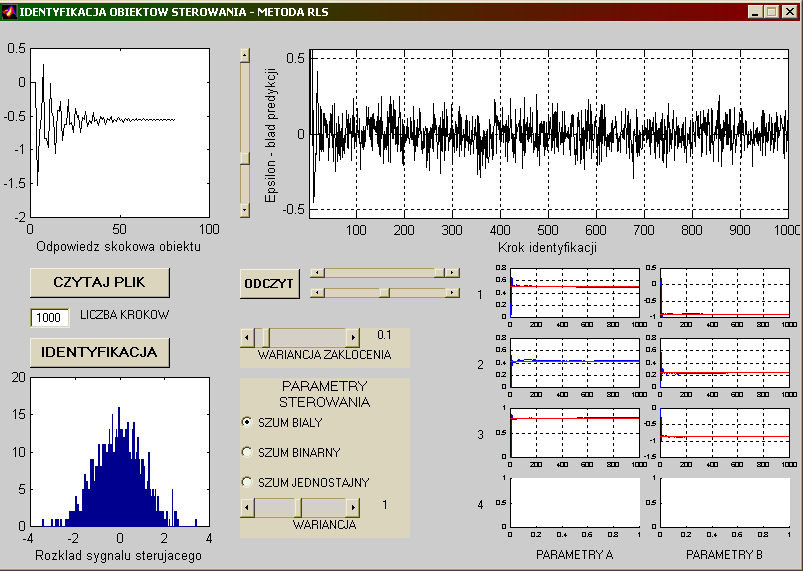
Tutaj zajmować się będziemy identyfikacją RLS – rekursywną metodą najmniejszych kwadratów. Rekursywna –
ponieważ działa w pętli iteracyjnej, najmniejszych kwadratów – ponieważ dążymy,
aby suma kwadratów uchybów była minimalna. Na razie zamieszczam screeny z
programów, jakie przyszło mi napisać w ramach przedmiotu identyfikacja obiektów
sterowania. Jeśli czas mi na to pozwoli, dalszy opis metod i zagadnienia identyfikacji będzie się stopniowo pojawiał na stronie.
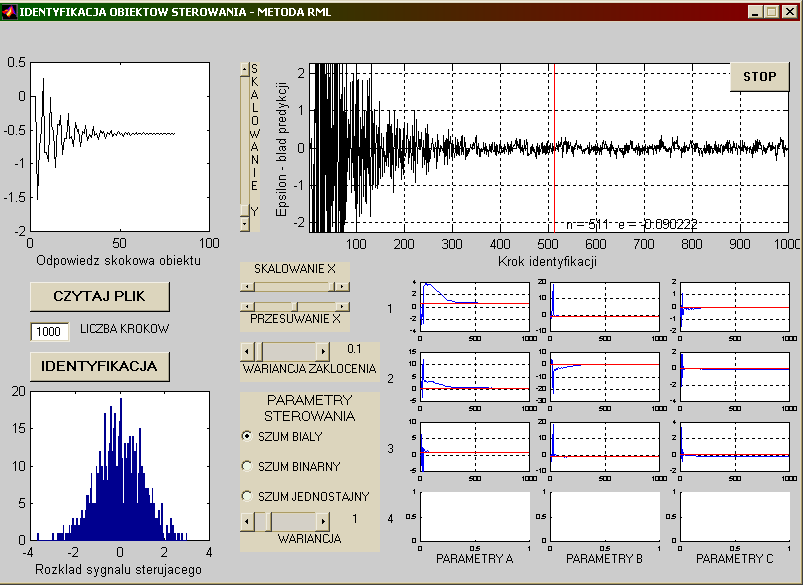
To samo zagadnienie w przypadku metody RML - największej wiarygodności:
Niedługo (mam nadzieję :)) opis algorytmów i budowy programu.
8. Dostęp do portów i innych urządzeń z poziomu Matlaba.
Z tym zagadnieniem spotkałem się przy
okazji tworzenia aplikacji pozwalającej na sterowanie kartą wejścia/wyjścia
Advantech PCI 1710. Program miał umożliwiać odczyt/zapis wejść
analogowych oraz cyfrowych. Niestety przy próbie skorzystania w Matlabie z
oryginalnego sterownika wynikły problemy, których nie udało się rozwiązać.
Tym sposobem autor zmuszony został do dostępu do karty bezpośrednio przez
jej rejestry. Tutaj mamy dwie możliwości: napisanie w C prostych funkcji
uzyskujących dostęp do przestrzeni wejścia/wyjścia komputera (z użyciem
na przykład poleceń outport, inport). Niestety cała idea pisania tych
tzw. funkcji MEX bierze w łeb w sytuacji, kiedy aplikacja będzie działać
w środowisku systemu operacyjnego klasy NT - są to systemy broniące dostępu
do portów i korzystanie z w/w poleceń nie daje rezultatu. Drugim sposobem
jest użycie któregoś z programików umożliwiających dostęp do portów.
Podczas szukania w sieci odpowiedniego programu natknąłem się na coś, co
idealnie nadawało się na potrzeby programu. Jest to wtyczka umożliwiająca
wysyłanie i pobieranie z portów wartości tak, jakbyśmy korzystali z
wbudowanych funkcji Matlaba (link do programu znajduje się w prawej
ramce).
STRONA W PRZYGOTOWANIU...
| matlab - linki |
 |
| :: Mathworld |
 |
| :: Matlab home |
 |
| :: Outport/inport pod matlabem |
 |
| ::
Komputerowo wspomagane projektowanie regulatorów prędkości i położenia |
 |
| :: |
 |
| :: |
 |
 |